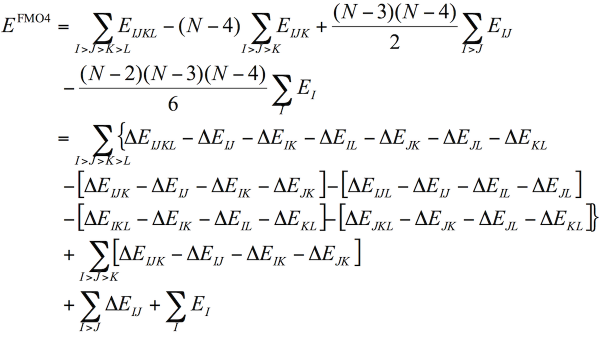東京大学生産技術研究所 革新的シミュレーション研究センター
鵜沢 憲 (uzawa@iis.u-tokyo.ac.jp)

背景
2016年8月3日に提供された64ビット版Windows10のバージョン1607(ビルド番号14393, Anniversary Update)から,Windows上でubuntu互換の実行環境(Windows Subsystem for Linux, 以降WSL)[1],及びシェル(Bash on Ubuntu on Windows, 以降BUW)が使用可能となった.
これまでWindows上で流体ソフトウェアを動かす場合,Windowsのバイナリで提供してもらって実行する,もしくはVMware[2], VirtualBox[3]等の仮想環境やCygwin[4]等のエミュレータでUNIXのバイナリを実行するようなケースがほとんどであろう.
Microsoft社のWSL開発グループによれば,それらの仮想環境と比較して,今回リリースされたWSLは必要とするリソース(CPU, メモリ, ストレージ)が少なくて済むと述べている[5].また,これまでの仮想環境やエミュレータで不便を感じることもあったWindowsとLinuxとの間でのファイルやディレクトリ,コマンドの互換性の問題も回避されている.これらの特徴は,Windowsで流体解析を行う際のハードルが下がる可能性がある.
そこで,試しにオープンソースの流体ソフトウェアをインストールし,流体解析の一連の流れを通じてWSLの使い勝手を調べるともに,簡単なベンチマーク問題を対象に計算性能を評価し,WSLにおける流体解析の可能性を調査することとした.
なお,流体ソフトは文科省フラッグシップ2020プロジェクト重点課題8「近未来型ものづくりを先導する革新的設計・製造プロセスの開発」サブ課題A「設計を革新する多目的設計探査・高速計算技術の研究開発」で開発が進められているFrontFlow/violet-Cartesian(FFV-C)[6]を用いた.FFV-Cは任意のアーキテクチャ対応の性能評価ライブラリPMlib[7]をデフォルトで実装しており,計算終了後に計算時間の測定や計算負荷のホットスポット同定等を検証することができる.
今回,PMlibを利用してWSLでの計算時間や計算性能について調査したところ,いくつか興味深い結果が得られたので,WSLの使用感とともに,まずは第一報としてここに報告する次第である.
WSL及びBUWのインストール及び動作確認
WindowsへのWSL及びBUWの導入手順や不具合,使用感などはこれまでに多く報告されている[8-11].
今回筆者も上記の手順をなぞることにしたが,日頃の行いが悪いのだろう,第一歩目のバージョン1607へのアップデートに失敗してしまった.プリインストールされていたWindows10 HomeにAnniversary Updateをかける度に,途中でフリーズしてしまうのである.頑張って心折れずに調べたところ,システムをSSDに入れているPCにアップデートをかけるとフリーズする場合がある[12] とのことで,今回の原因もどうやらそのようであった.
対処方法として,今回はプリインストールされていたWindows10を完全に削除し,イメージ形式で取得したバージョン1607[13]をUSBからクリーンインストールすることとした.クリーンインストール後は,上記の記事通りになぞることで,無事WSL及びBUWを入手することができた.
インストールが上手くいくと,スタートメニューに「Bash on Ubuntu on Windows」が現れるようになる(図1).インストール時間を正確に測定したわけではないが,感覚的には,従来の仮想環境やエミュレータ環境を構築する場合と比較してはるかに短時間かつ容易に構築することができた.一般的なWindowsアップデートに毛が生えた程度の印象である.
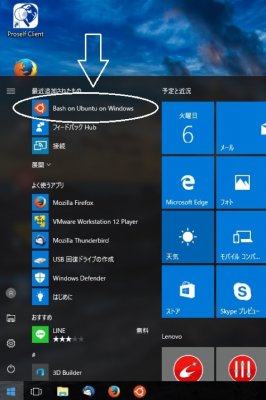
図1Bash on Ubuntu on Windows on スタートメニュー
クリックすると,普段使っているubuntuと同様のbashが立ち上がった.ubuntuとbashのバージョンは,それぞれ14.04と4.3.11である.(図2)
図2 夢にまで見たWindowsでのbash
BUWを一通り触り,ネイティブbashと同様の操作感であることを確認.
FFV-Cのインストール及び動作確認
引き続き,流体ソフトウェアのFFV-Cをインストールする.なお,WSLには必要最低限の機能しか入っていないので,FFV-Cの計算やプリ・ポスト処理に必要なソフトウェアやライブラリを予めインストールしておく.
GNUコンパイラ(gcc, g++, gfortran)及びgnuplotのインストール
ネイティブubuntu下と同様に,それぞれsudo apt-get install * とすれば良い.
$ sudo apt-get install build-essential
$ sudo apt-get install gfortran
$ sudo apt-get install gnuplot-x11
(もちろん,まとめてインストールしても良い.)
なお,sudo実行時に「***の名前解決ができません」と出るときは,WindowsのIPアドレスをetc/hostsに記入すれば,毎回怒られずに済む.(図3)
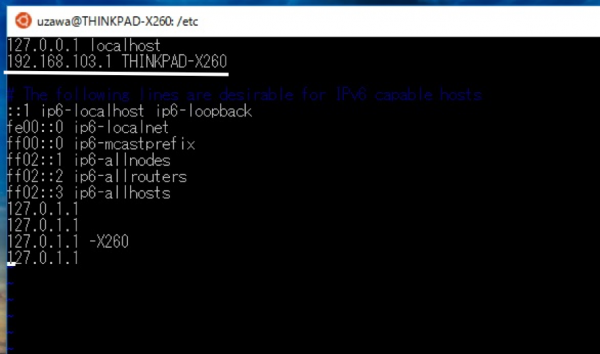
図3 /etc/hosts ファイル
OpenMPIのインストール
FFV-Cは,OpenMPIによるプロセス並列とOpenMPによるスレッド並列を組み合わせたハイブリッド並列でコーディングされている.したがって,OpenMPIのソースコードを公式サイト[14]等から入手し,所望のディレクトリ下で展開,コンパイル・実行しておく.
この際configure用に以下のスクリプトを用意しておくと便利である[15].
$ vi config.sh
#!/bin/bash
export CC=gcc
export CFLAGS=-O3
export CXX=g++
export CXXFLAGS=-O3
export F77=gfortran
export FFLAGS=-O3
export FC= gfortran
export FCFLAGS=-O3
./configure --prefix=$1
問題なくconfigureできたら,コンパイルとインストールをする.
$ make
$ make install
MobaXterm のインストール
プリ・ポスト処理のために,Windows上の代表的なXサーバであるMobaXterm[16]をインストールする.MobaXtermをインストールしておくと,入力ファイルを外部エディタで修正したり,計算結果を可視化したりできるようになるので便利である.
インストールはほぼ一直線なので割愛する.無事にインストールが完了すると,MobaXtermを立ち上げることができる.(図4)
図4 MobaXterm の初期画面
MobaXterm を確認すると,WindowsのIPアドレスが192.168.103.2:0.0と表示されているので,BUW側で
$ export DISPLAY=192.168.103.2:0.0
と設定する.これでXサーバが利用可能になる.
V-Isio のインストール
ポスト処理のために,軽量のオープンソース可視化ソフトウェアV-Isio[17]もインストールしておく.手順は以下の通り.
alien パッケージのインストール
$ sudo apt-get install alien
alien で rpm 形式のパッケージを deb 形式に変換
$ sudo alien Visio-2.4-6.el6.x86_64.rpm
成功するとvisio_2.4-7_amd64.debができる.
deb パッケージのインストール
$ sudo dpkg -i visio_2.4-7_amd64.deb
パスを通す
$ export PATH=/usr/local/Vtools/bin:$PATH
事前に足りないライブラリを入れておく
$ sudo apt-get install libgtk2.0-0
$ sudo apt-get install libpangox-1.0-0
$ sudo apt-get install libjpeg62
これでも
$ Visio: error while loading shared libraries: libtiff.so.3:
cannot open shared object file: No such file or directory
と怒られるので,libtiff.so.* を適当に探し,シンボリックリンクを作成する.
$ sudo find . -name libtiff.so.*
$ ./usr/lib/x86_64-linux-gnu/libtiff.so.5
$ sudo ln -s /usr/lib/x86_64-linux-gnu/libtiff.so.5 \
/usr/lib/x86_64-linux-gnu/libtiff.so.3
$ Visio
アクセス許可を求めるポップアップが出るが,ここで「はい」とすることで,無事にV-Isioが立ち上がる.(図5)
図5 V-Isio の初期画面
今回は割愛するが,V-Isioの他にも,ParaViewやVisIt等の可視化ソフトウェアもインストールできるので,必要に応じて試して頂きたいと思う.
FFV-Cのインストール
GNU コンパイラ(もしくは Intel コンパイラ)と OpenMPI があれば FFV-C のインストールが可能になる.
$ http://avr-aics-riken.github.io/ffvc_package/
で最新版FFV-C(バージョン2.4.3)をtar.tz形式もしくはzip形式でダウンロードしたのち,所望のディレクトリに展開し,インストール.
なお,FFV-C には GNU 環境用と Intel 環境用の両方に自動インストールスクリプトが付属しているので,これを利用すると良い
$ tar xvfz avr-aics-riken-ffvc_package-x.x.x.tar.gz
$ cd avr-aics-riken-ffvc_package-x.x.x
$ ./install_intel.sh
お茶を一杯飲んでいる間にインストールが終わる.
試しに組み込み例題の2次元キャビティ問題を計算する.プリ処理としてviエディタで入力ファイルに問題ないことを確認した後,実行.
無事にFFV-Cが動作することが確認できた.(図6)
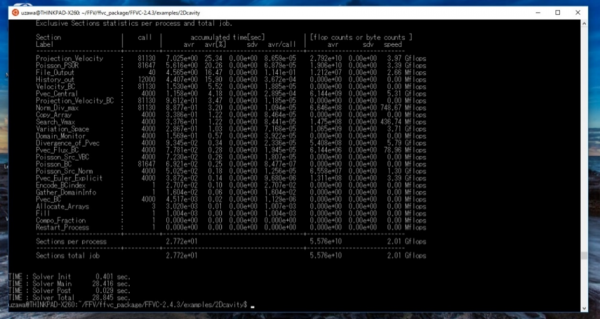
図6 FFV-C on Bash on Ubuntu on Windows
計算ログをgnuplotで確認.(図7)
速度の発散値や相対残差ノルム値の時間発展を確認し,収束性に問題がないかどうかを確認する.
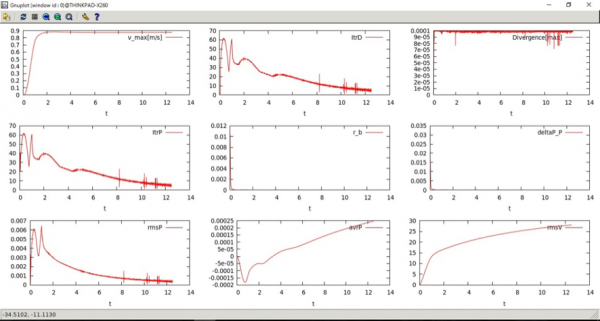
図7 gnuplot を用いた計算ログの表示
速度の絶対値をV-Isioで可視化してみる.(図8)
物理的に奇妙な挙動を示していないことを確認する.
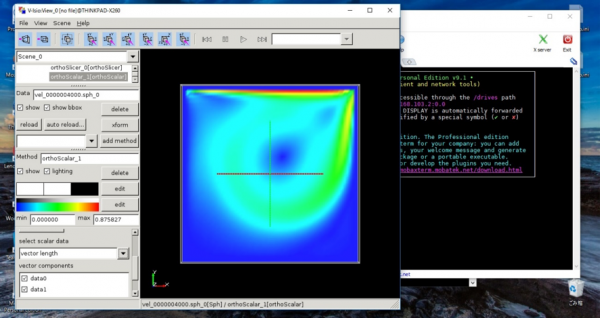
図8 2次元キャビティ問題における速度の絶対値のプロット図.ubuntuにインストールしたV-Isioで可視化.
ここまでで,プリからポストまでの一連の流体解析が問題なく実行できることが確認できた.
ところで,今回のWSLで筆者が個人的に大変便利だと感じていることは,ubuntuのファイルやディレクトリをWindows操作できる点である.このことにより,一連の流体解析の操作性が従来の仮想環境やエミュレータと比較して格段に向上している.本稿はこのために書いたといっても過言ではない.
WSLは,Windowsのファイルシステムの
C:¥Users¥「username」¥AppData¥Local¥lxss
に格納されている.(図9)
ただし,これを見るためには,「エクスプローラー」→「オプション」→「フォルダーと検索のオプションの変更」→「フォルダーオプション」→「表示」で,「保護されたオペレーティングシステムファイルを表示しない(推奨)」のチェックを外しておく必要がある.(図10)
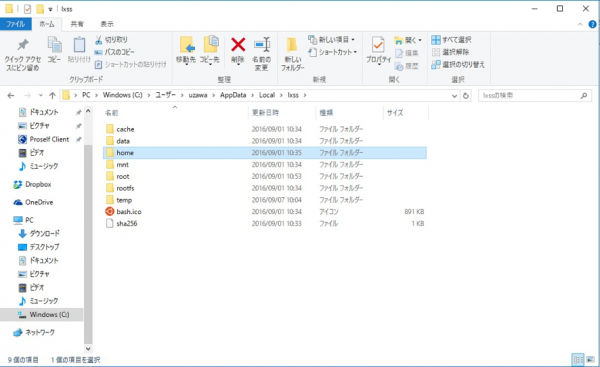
図9 Windowsファイルシステム内のWSL格納箇所
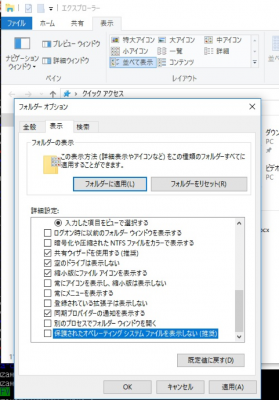
図10 フォルダーオプション内のチェックを外す
すると,計算ディレクトリをWindows側からも見ることができるようになる.(図11)
Windows側からはファイルがフルコントロールになっているので,入力ファイルをWindows側のエディタで操作することもできる.(図12)これは,ちょっとした感動である.リンクを張っておくと,さらに操作性は向上する.もちろん,ファイルやディレクトリの名前変更や移動等も可能になっている.
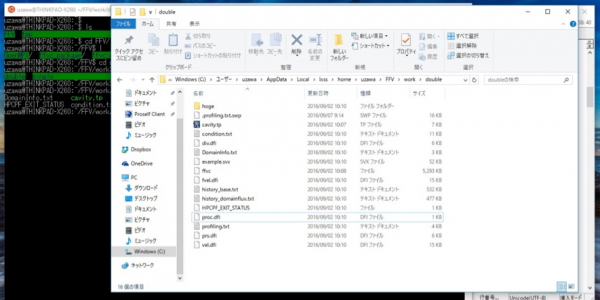
図11 Windows から ubuntu のディレクトリが丸見え
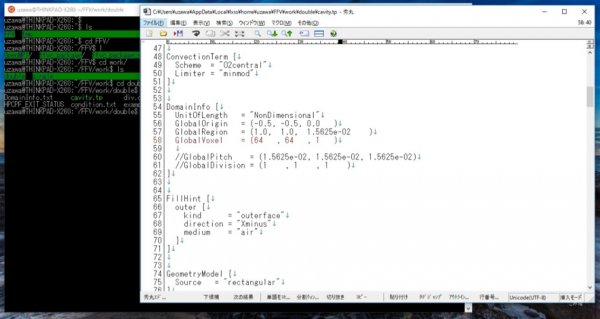
図12 Windows のエディタで ubuntu の入力ファイルを直接編集することができる
同様に,Windowsファイルシステム内のファイルを読み込んで可視化することができる.先程はWSL内のV-Isioで可視化したが,今度はWindowsにインストールしたV-Isioで可視化してみる.V-Isioを立ち上げて,Windowsファイルシステム内のファイルを選択する.(図13)
すると,問題なくWindows側のV-Isioで可視化することができた.(図14)
当然だが図8と同様の可視化結果が得られている.
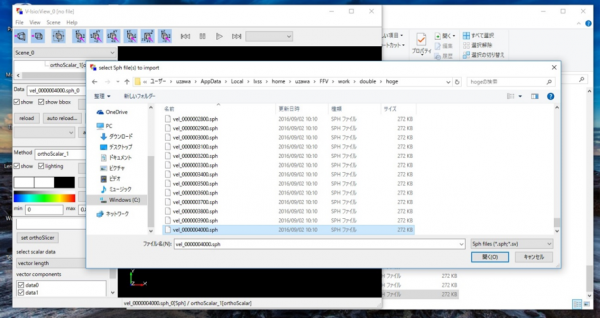
図13 Windows のV-Isioでubuntuの可視化データを直接読み込む
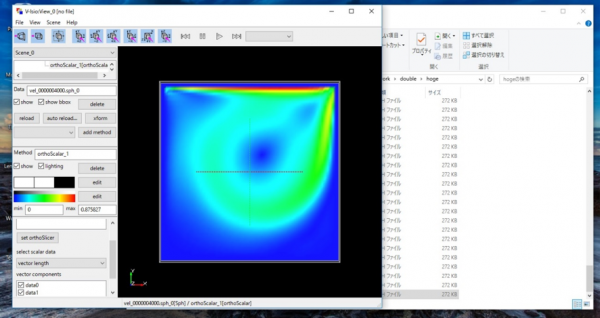
図14 2次元キャビティ問題における速度の絶対値のプロット図.Windows にインストールしたV-Isioで可視化.
性能評価結果
これまでに,プリからポストまでの一連の流体解析を通じ,従来の仮想環境やエミュレータと同等以上の操作性を実感した.
とは言っても,計算性能に難があるようではやはり実用的には使い物にならないため,簡単にWSL上での計算時間や実行性能を調査することとした.
方法として,仮想環境(VMware)上にWSL環境と同一のバージョンのubuntuとFFV-Cを用意し,計算時間や計算性能を両者で比較した.ベンチマークテストとしては,2次元キャビティ問題を選んだ.総セル数は64×64×1=4096であり,圧力ポアソン方程式の反復法は点過緩和SORで,反復回数は最大20回とし,相対残差の閾値は10-4とした.なお,MPIプロセス数は1とし,スレッド数は4とした(図15中の(1)).
それぞれのプロファイルレポートを,図15と図16に示す.
Total execution time (マスタープロセスの経過時間)を両者で比較すると,後者が約3.80秒なのに対し前者は2.78秒で済んでおり,WSLでの計算が約1.37倍早いことが分かった(図15, 16中の(2)).総計算時間に対する各サブルーチンの割合を調べると,どちらの場合にも上位2つはProjection_Velocityと,Poisson_PSORであり(図15, 16中の(3)),これはどちらもフラクショナルステップの一部であり,ナビエ-ストークス方程式の演算部分にあたる.flop counts or byte counts 欄を見ると,どちらのサブルーチンもWSLのほうが1.1-1.2倍程度高い実効性能が出ていることが分かり,WSLは仮想環境と比較して独自のOSを立ち上げる必要がないためにCPUやメモリ等のリソースを有効活用されていることが示唆される.
その一方で,WSLでのFile_Outputはたった40回のコールで総計算時間の20パーセント弱を食っており,実効性能値を見てもVMwareでのそれと比較して1/10以下であることが分かった.他のファイルI/Oサブルーチンである History_outも同様の傾向を示しており,WSLでのファイルI/Oの性能がVMwareでのそれと比較して,極めて高コストであることを示している.
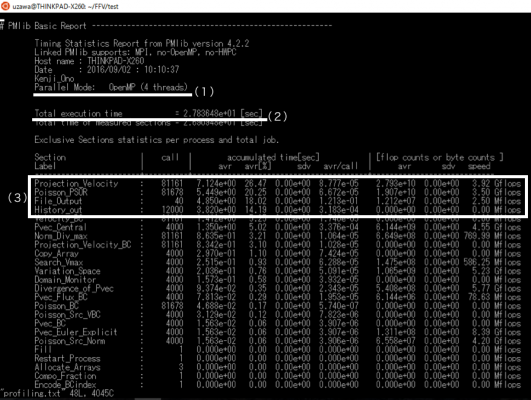
図15 プロファイルレポート(WSL)
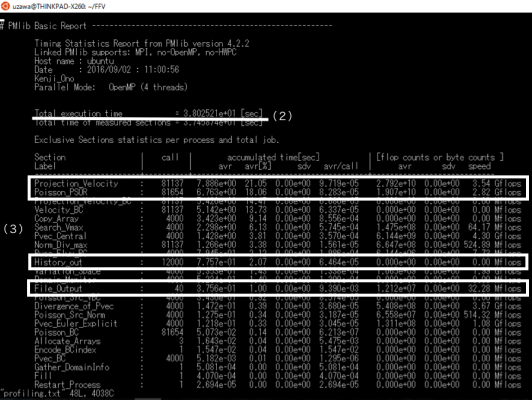
図16 プロファイルレポート(VMware)
まとめ
Windows10上の ubuntu互換環境(Windows Subsystem for Linux, WSL)にオープンソースの流体ソフトウェアFFV-Cをインストールし,流体解析の一連の流れを通じてWSLの使い勝手を検証するともに,流体ソフトウェアの簡単な性能評価を行い,WSLにおける流体解析の可能性を調査した.
FFV-Cのインストールでは,必要とされるライブラリやソフトウェアがほとんどubuntuネイティブ環境下と同等であることが分かった.また,プリからポストまでの一連の流体解析も,従来のubuntuネイティブ環境下と全く同様に実行できることが確認できた.
もっとも,記事執筆時(2016/9/9)において WSLはベータ版であり,64ビット版限定での提供やシェルの日本語が一部文字化けする等,多少機能に不十分な点も見受けられた.しかし, Microsoft社の本気度(開発項目の優先順位などは[5]参照),導入の容易さ等から考えると,近い将来に従来の仮想環境やエミュレータを脅かす,ないしは置き換える存在になり得るものと考えている.
2次元キャビティ問題を対象にWSLの計算性能を調査した.その結果,WSLでの計算が従来の仮想環境での計算と比較して約1.37倍早いことが分かった.これは,WSLが仮想環境と比較して独自のOSを立ち上げる必要がないため,CPUやメモリ等のリソースが有効活用されていることを示唆している.一方で,WSLのファイルI/Oの実効性能値がVMwareでのそれと比較して1/10程度に留まり,WSLのファイルI/Oが極めて高コストであることが分かった.WSLでの計算では,以上の特性を留意しておく必要があると考えられる.今後は,プロセス/スレッド数依存性の調査や,他のオープンソース流体ソフトウェア(FrontFlow/BlueやOpenFOAM等)を対象とした同様の検証を行うことも検討したい.
近年,PCの性能向上や計算手法・格子生成技術の発達等により,ある程度大規模な計算がローカルPCでも可能になってきた.一般に業務用PCはWindowsマシンであるが,プリからポストまでの流体解析をほぼWindows操作することが可能なubuntu互換環境WSLを用いることで,従来の流体解析がさらに身近になったのではないかと考えられる.
参考文献およびウェブサイト
[1] https://msdn.microsoft.com/en-us/commandline/wsl/about
[2] http://www.vmware.com/jp.html
[3] https://www.virtualbox.org/
[4] https://www.cygwin.com/
[5] https://msdn.microsoft.com/en-us/commandline/wsl/faq
[6] http://avr-aics-riken.github.io/ffvc_package/
[7] https://github.com/avr-aics-riken/PMlib
[8] http://pc.watch.impress.co.jp/docs/column/nishikawa/1017333.html
[9] http://www.atmarkit.co.jp/ait/articles/1608/08/news039.html
[10] http://rcmdnk.github.io/blog/2016/06/05/computer-windows-ubuntu-bash/
[11] http://cabonera.hateblo.jp/entry/2016/08/04/003300
[12]http://answers.microsoft.com/ja-jp/windows/forum/windows_10-performance/anniversary-update/66e03b07-4845-4a66-be07-0feda12bd34e
[13] https://www.microsoft.com/ja-jp/software-download/windows10
[14] https://www.open-mpi.org/
[15] User Guide of FFV-C Frontflow/violet Cartesian
[16] http://mobaxterm.mobatek.net/
[17] http://avr-aics-riken.github.io/V-Isio
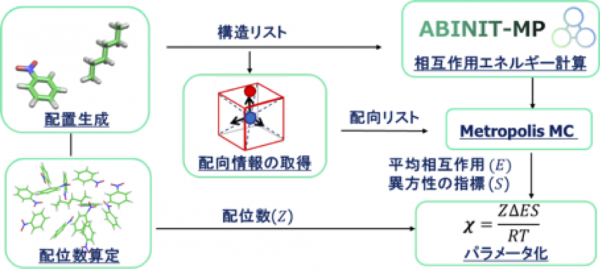










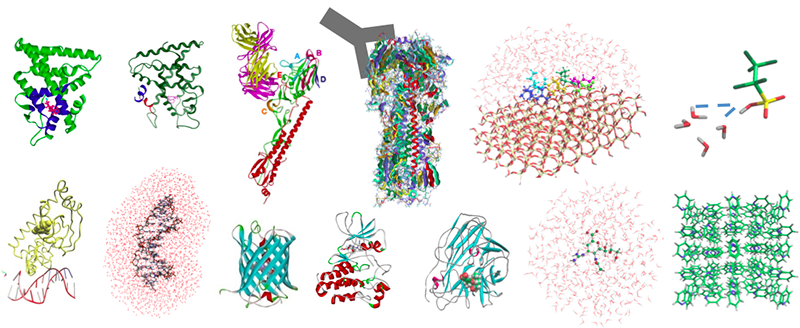
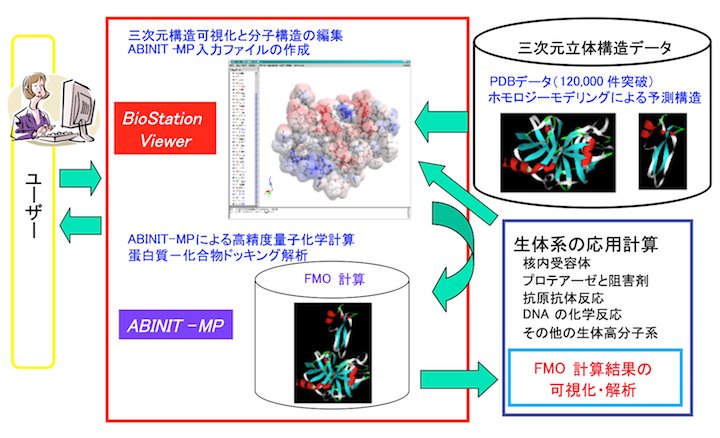
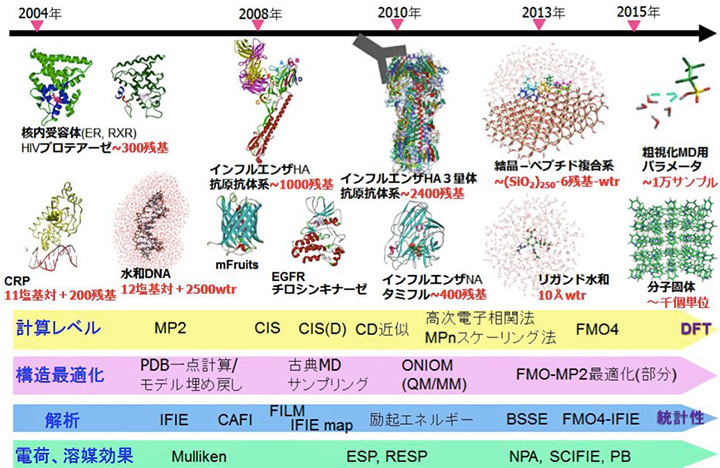
 ABINIT-MPは、フラグメント分子軌道(FMO)計算を高速に行えるソフトウェアです[1]。専用GUIのBioStation Viewerとの連携により、入力データの作成~計算結果の解析が容易に行えます。4体フラグメント展開(FMO4)による2次摂動計算も可能です。また、部分構造最適化や分子動力学の機能もあります。FMOエネルギー計算では、小規模のサーバから超並列機の「京」まで対応しています(Flat MPIとOpenMP/MPI混成)。
ABINIT-MPは、フラグメント分子軌道(FMO)計算を高速に行えるソフトウェアです[1]。専用GUIのBioStation Viewerとの連携により、入力データの作成~計算結果の解析が容易に行えます。4体フラグメント展開(FMO4)による2次摂動計算も可能です。また、部分構造最適化や分子動力学の機能もあります。FMOエネルギー計算では、小規模のサーバから超並列機の「京」まで対応しています(Flat MPIとOpenMP/MPI混成)。