RaspberryPiクラスタ製作記 第3回「並列プログラミング」
第3回 並列計算プログラムをつくろう

前回までは既存のプログラムを使い、並列化による性能上昇について調べました。これにより大雑把に「並列化するとプログラムの処理を高速化できる」ことはわかりましたが、具体的にどのようにすれば自分のプログラムを並列化して高速化できるのかは、まだわかりません。
そこで今回からは、連立一次方程式を解くプログラムの制作を通して、並列計算プログラムを1から自作する方法や、高速化のための手法について学んでいきたいと思います。
なぜ連立一次方程式を扱うかというと、それは理解が容易だからです。スパコンでは様々な計算が行われていますが、大抵これらの計算は非常に難しく、短時間で理解し、プログラムを作るのは大変です。しかし、連立一次方程式は小さいサイズなら筆算で簡単に解けるため、これを解くプログラムの理解も容易です。加えて、連立一次方程式をプログラムで解く方法は、数値計算の教科書や並列計算の入門本など、非常に多くの書籍で扱われています。 そのため、内容でわからないことが出た場合や、より詳しく知りたい場合などは、豊富な参考文献をあたって調べられます。
本記事も、片桐孝洋さんの『スパコンプログラミング入門 並列処理とMPIの学習』という本と、同じく片桐さんの講義資料を参考にしています。わからないことが出た際はこちらを参照してください。
LU分解法(1)
LU分解法(2)
LU分解法(3)
東京大学情報基盤センター 准教授 片桐孝洋
連立一次方程式をプログラムで解く
今回は「LU分解」を用いて、以下の簡単な連立一次方程式を解くプログラムを作っていきます
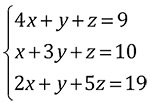
一般に、問題を解くプログラムのことをソルバと呼び、今回の連立一次方程式を解くプログラムのことは連立一次方程式ソルバと呼びます。
LU分解のアルゴリズムはいくつかあります。 今回は片桐さんの資料でも並列化に向くと紹介されている、外積形式ガウス法を用いて計算を行います。
※外積形式ガウス法を用いたLU分解のアルゴリズムについては下記のページを参照してください
アルゴリズムのおさらい
行列の定義
係数行列A、変数ベクトルx、定数項b、ベクトルcはプログラムで次のように定義します。
// SIZE: 係数行列Aのサイズ
#define SIZE 3
double A[SIZE][SIZE] = {
{4, 1, 1},
{1, 3, 1},
{2, 1, 5}
};
double b[SIZE]={9,10,19};
double c[SIZE];
double x[SIZE];
LU分解のコードを作る
最初に係数行列Aを下三角行列Lと上三角行列Uに分解するコードを作ります。
下三角行列Lと上三角行列Uは一般的に1つの行列で表されます。
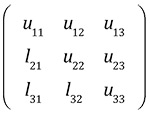
行列LUの要素は、LU分解より係数行列Aを更新しつつ作られるので、 係数行列Aに上書きして入れていきます。 そして、LU分解が完了すると、行列Aの中身はすべて行列LUの要素におきかわります。 その後の前進代入と後進代入は、行列Aを置き換えて作られた行列LUを用いて行います。
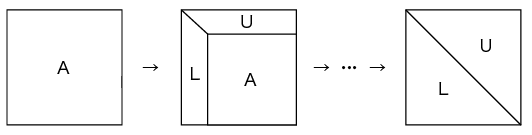
外積形式ガウス法を用いたLU分解は、 行方向のループk(k=0,1,…,n=SIZE)と、 そこに入れ子になった以下の2つのループで行います。
・行列L(枢軸ベクトル)を作っていく列方向のループ……(1)
・行列Uを作り、残りの値を更新する行と列の2重ループ……(2)
です。
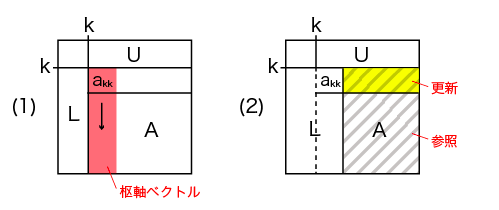
この時、1つ目のループで計算されるベクトルのことを枢軸(すうじく)ベクトルと呼びます。
以上の処理をプログラムで表すと、次のようになります。
int n = SIZE;
// LU分解開始
for (k=0; k<n; k++) {
// kで回す行方向ループ
// (1)
// 行列Lの処理
double div_tmp = 1.0 / A[k][k];
for (i=k+1; i<n; i++) {
// iで回す行方向ループ
// l_ik = a_ik / a_kk
A[i][k] = A[i][k] * div_tmp;
}
// (2)
// 行列Uの処理
for (j=k+1; j<n; j++) {
// jで回す行方向のループ
// Tips: ここで値を変数に入れたほうが
// ループ内で参照するよりメモリアクセス回数が減ってお得
double a_jk = dtemp = A[j][k];
for (i=k+1; i<n; i++) {
// iで回す列方向のループ
A[j][i] = A[j][i] - A[k][i] * a_jk;
}
}
}
// LU分解終了
前進代入
LU分解の後は下三角行列Lと定数項bの値より、Lc=bのベクトルcの値を求めます。
// 前進代入
// Lc = b
for(k=0; k<n; k++){
// 行方向のループ
c[k] = b[k];
for(i=0; i<k; i++){
// 列方向のループ
c[k] -= A[k][i] * c[i];
}
}
後進代入
前進代入で求めたベクトルcより、Ux = cを解いて変数ベクトルxを求めます。
// 後進代入
// Ux = c
// k = n - 1
x[n-1] = c[n-1] / A[n-1][n-1];
// k = (n - 2) ~ (0)
for(k = n - 2; k >= 0; k--){
x[k] = c[k];
for(i=k+1; i<n; i++){
// 列方向のループ
x[k] -= A[k][i] * x[i];
}
x[k] = x[k] / A[k][k];
}
完成
以上でLU分解を用いた連立一次方程式ソルバは完成です。 以下にコードを示します。
このコードを実行すると、式eq01の係数行列AをLU分解した結果と、変数ベクトルxの解が出力されます。
$ gcc -o LU_normal LU_normal.c $ ./LU_normal LU: 4.00 1.00 1.00 0.25 2.75 0.75 0.50 0.18 4.36 x: 1.00 2.00 3.00
LU分解コードを並列化しよう
ここからはMPIを用いて、連立一次方程式を並列に解くプログラムを作っていきます。 ただし全ての並列化を行うのは大変なので、計算に一番時間がかかるLU分解の部分のみを並列化します。
※MPIについてご存じない方は、以下のページを参照してください。
MPIを用いた並列プログラミングの概要
最初に完成したコードを示し、このコードを扱いながら説明を行います。 以下からダウンロードして下さい。
担当範囲の計算
外積形式ガウス法を用いたLU分解の並列化を、今回は列方向に分割して行います。
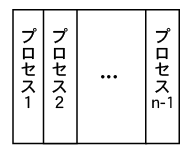
各プロセスはそれぞれ、以下のプログラムで計算した、 開始(start)から終了(end)までの列を担当し、計算します。 担当列の長さは(partition_size)で表します。
// 1つのプロセスが担当する列の長さ int partition_size = n / numprocs; // プロセスが担当する列の開始点 int start = myid * partition_size; // プロセスが担当する列の終了点 int end = (myid + 1) * partition_size;
行列Lの計算と放送
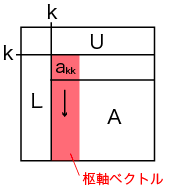
下三角行列L(枢軸ベクトル)の計算は、その列を担当するプロセスが行います。
枢軸ベクトルは、その他のプロセスが係数行列Aの更新に必要とするので、別のプロセスに放送します。 そのため、枢軸ベクトルを担当したプロセスは、 別途放送用の配列Lを用意し、更新した値を配列Lに入れて放送します。
この処理を行うのが、次のコードです。
int worker = k / partition_size;
// 行列Lの処理
if(worker == myid){
// kが自分の担当範囲内の場合はLを処理
double div_tmp = 1.0 / A[k][k];
for (i=k+1; i<n; i++) {
// iで回す行方向ループ
// l_ik = a_ik / a_kk
A[i][k] = A[i][k] * div_tmp;
L[i] = A[i][k];
}
}
// Lを放送
MPI_Bcast(&L[k], n - k, MPI_DOUBLE, worker, MPI_COMM_WORLD);
行列Uを計算する
枢軸ベクトルを受け取った各プロセスは、行列Uの計算と、行列Aの値の更新を行います。

最初に行うのは、計算に使用する枢軸ベクトルの要素a_jkの取り出しです。
double a_jk = L[j];
次に自身の担当する列のみ計算するため、i-ループを次のように書き換えます。
if(k < start){
i = start;
}
else{
i = k+1;
}
for (; i < end; i++) {
// 行列Uの計算と更新処理
kがプロセスの担当列番号より小さい場合は、startからendまでループを回して計算します。
その他の場合はkが自分の担当範囲か、自分の担当範囲が既に終了しているので、k+1からendまでループを回して計算します。
以上でLU分解の処理は終了です。
結果を集計する
今回の並列化はLU分解のみとしているので、 LU分解後の処理はすべてプロセス0が行います。 そのため、LU分解後は各プロセスの計算した配列LUのデータを、プロセス0に集めます。
これを行うのが次のコードです。
/ 結果を集める
for(i = 0; i < n; i++){
// 行方向のループ
for(j = partition_size; j < n; j+=partition_size){
// 列方向のループ
int worker = j / partition_size;
if(myid == 0){
// process0 はその他のプロセスの担当部分を集める
MPI_Recv(&A[i][j], partition_size, MPI_DOUBLE, worker, 0, MPI_COMM_WORLD, &istatus);
}
if(myid == worker){
// process0 以外は、自分が担当した部分を送る
MPI_Send(&A[i][j], partition_size, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
}
// すべてのプロセスがここに来るのを待つ
MPI_Barrier(MPI_COMM_WORLD);
}
}
性能測定
プログラムの並列化は少々大変でしたが、 このプログラムを複数ノードで並列に動かすことで、 高速に計算できるはずです。
係数行列のサイズは3程度では変化がわからないので、 サイズを192に拡大して実行しました。 その結果をグラフに示します。
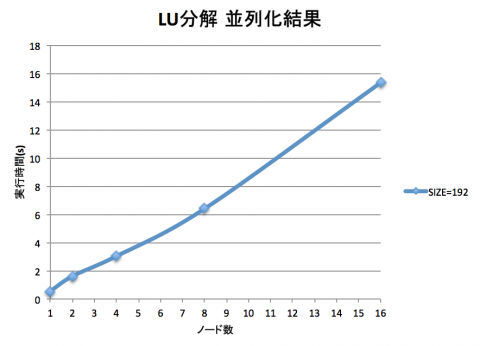
PHASE/0のときのようにノード数が増えるごとに計算時間が減って……いませんね。 今回のプログラムはPHASE/0の時と真逆で、ノード数を増やすごとに処理時間が増えています。
どうやらLU分解を並列化しただけでは、並列化のコスト(主に通信のコスト)のほうが大きいため、逆に時間が増えてしまうようです。
残りの前進代入と後進代入も並列化すれば、ノード数に応じて処理時間が減っていく、期待通りの結果が得られるかもしれません。余力のある方は、最初に挙げた片桐さんの資料を参考に、並列化を行ってみてください。私は別の方法で高速化を図ってみます。
BareMetalで作る連立一次方程式ソルバ専用機
現代のOSは様々な機能を私たちに提供してくれています。マルチタスクシステムもその1つです。このシステムは同じマシンを複数の人が使うことを想定し、プロセスを人間が分からない程度の短時間で切り替え、あたかも複数のプログラムが同時に動いているかのように実行するシステムです。これのおかげで私たちは先程のLU分解のプログラムを動かしている間も、別マシンからSSHアクセスして作業することが可能になっています。
しかし、今回のように私1人が1つのプログラムだけを処理したい場合、マルチタスクシステムを含め、OSの便利な機能は必要のない、無駄な機能です。このマルチタスク処理を含め、OSの実行にかかる様々なコストを削減して高速化できないでしょうか。
私はこの目的を達成する方法に、心当たりがあります。著者紹介欄でもご紹介頂いているように、私は「Baremetalで遊ぶ Raspberry Pi」という電子書籍を書きました。
通常Raspberry Piは、電源投入後にSDカード上のプログラムを読み込み、 LinuxなどのOS(カーネル)を起動します。 ここで、SDカード上の設定を少し書き換えると、本来カーネルが起動するところを、代わりに自作のコードを実行できます。そうすればOSの実行にかかる様々なコストを削減して、計算を高速に行えるはずです。
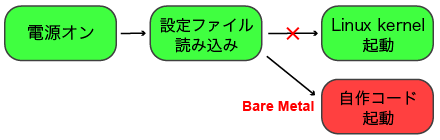
この自作のコードの作り方と、OSを用いない素のハードウェア(BareMetal)上で、 Raspberry Piを制御する方法を説明した電子書籍が「Baremetalで遊ぶ Raspberry Pi」です。
ここからは前半に作った連立一次方程式ソルバをBareMetal上に再実装して、高速化を測ります。これはいわば、Raspberry Piを1次方程式を解くための専用機として運用するようなものです。このような贅沢な使い方ができるのも、自作スパコンの特権です。
早速、製作を行っていきましょう。
クロスコンパイル開発環境を整える
プログラムのバイナリを動かす環境と、コンパイルを行う環境が異なるコンパイルのことを、クロスコンパイルといいます。 BareMetal開発を行うには専用のクロスコンパイル開発環境が必要なので、 これから用意していきます。
以降の作業をRaspberry Piで行うと、最低でもまる1日以上かかってしまいます。 なので性能の良い別のマシン上(以降、母艦)にクロスコンパイル環境を用意します。
環境を合わせるため、母艦のOSはDebian Linux(wheezy) x86_64版を用います。 他の環境を使われている方は、仮想マシン上にこの環境を用意して行ってください。
Crosstool-NGのインストール
クロスコンパイル環境作成は、Crosstool-NGというツールを使って行います。 以下のコマンドを実行してインストールしてください。
$ wget http://crosstool-ng.org/download/crosstool-ng/crosstool-ng-1.20.0.tar.bz2 $ tar jxvf crosstool-ng-1.20.0.tar.bz2 $ cd crosstool-ng-1.20.0 $ ./configure $ make $ sudo make install
クロスコンパイラのビルド
ここからはCrosstool-NGを使ってクロスコンパイル環境を作成します。 作成に必要な設定ファイルを以下からダウンロードして、母艦のホームディレクトリに保存してください。
ダウンロード完了後、 以下のコマンドを実行すると、 クロスコンパイル環境のビルドが始まります。 環境にもよりますが、ビルド完了までは大体30分以上かかります。 気長にお待ちいただければと思います。
$ mkdir -p ~/ct-ng-rpi/src $ cd ~/ct-ng-rpi $ ct-ng arm-unknown-eabi $ mv ~/hard_dot_config .config $ ct-ng build
パスの追加
作成の終わったクロスコンパイル環境は ~/cross/arm-hardfloat-eabi 以下に保存されます。 このツールを使えるよう、システムにパスを通します。 以下のコマンドを実行してください。
$ export PATH=$PATH:$HOME/cross/arm-hardfloat-eabi/bin $ echo 'export PATH=$PATH:$HOME/cross/arm-hardfloat-eabi/bin' >> ~/.bashrc
これで開発環境は整いました。
プログラムのクロスコンパイルとインストール
BareMetal環境上ではOSのもつ資源が一切ないので、 初期状態ではprintfどころかC言語自体がまともに動きません。
この問題を解決するには自分で初期化コードを書く必要があります。しかし、この作業は今回の本質でないので省略して、著書のコードをベースに開発を行います (この内容について興味のある方は、著書を読んでいただけると嬉しいです)。
以下に著書のコードをベースとして、 今回作成したLU分解の連立一次方程式ソルバをMyLUsolver関数として実装したコードを示します。次のリンクからダウンロードして下さい。
クロスコンパイル
先ほどダウンロードしたコードをクロスコンパイルして、 BareMetal Raspberry Piで動くコードを生成します。
コードにはMakefileを用意してあるので、makeコマンドでコンパイルは完了します。
$ make
実際に動かすバイナリの名前は rpi-micon.imgです。
インストール
Raspberry Piは起動時に、第1パーティションの設定ファイル config.txt を読み込んで、各種初期設定を行います。 この設定ファイルを書き換えると、起動時に読み込むプログラムを書き換えられます。
ここからはその設定ファイルを書き換え、自作コードが動くように設定を行います。 Raspberry Piに刺していたSDカードを抜き、パソコンに接続してください。
するとこのようにBOOT(第1パーティション)とRECOBERYの2つのパーティションが見えるはずです。
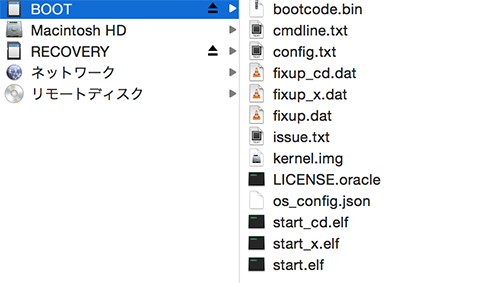
BOOTパーティションを開くと、中にconfig.txtが見つかります。 このファイルの末尾に、以下の1行を追記してください。
kernel=rpi-micon.img
これでRaspberry Piは、第1パーティションのrpi-micon.imgを起動するようになります。
最後にrpi-micon.imgを母艦からSDカードに移せばインストールは完了です。
シリアル通信
BareMetal環境上の標準出力はRaspberry PiのUART(シリアル通信)に出ていて、信号レベルは3.3Vです。 これを母艦で読み取るため、USB-シリアル変換ケーブルとRaspberry Piを接続します。
※シリアルケーブルはFTDI社のケーブル(秋月電子)がお勧めです。
Raspberry PiのUARTはP1コネクタのGPIO14番からTX、GPIO1510番からRXが出ています。

上記の図と、USB-シリアル変換ケーブルの仕様を参照して
・Raspberry PiのTXをUSB-シリアル変換ケーブルのRX
・Raspberry PiのRXをUSB-シリアル変換ケーブルのTX
・Raspberry PiのGNDをUSB-シリアル変換ケーブルのGND
に接続してください。
シリアル通信を行うプログラムは、Windowsの方はTeraTerm、Macの方はCoolTermをおすすめします。ボーレートは115200bpsに設定してください。
BareMetal版の性能測定
SDカードをRaspberry Piに刺し電源を起動するとプログラムが動作し、連立一次方程式の解と実行時間を出力します。
最初に比較のため、Linux上で動かした連立一次方程式ソルバの結果を示します。 コードは以下からダウンロードして下さい。
$ gcc -O2 -o LU_normal_192x192 LU_normal_192x192.c $ ./LU_normal_192x192 exec time: 0.380212(sec)
結果は380ミリ秒でした。 これに比べてBareMetalでは、はたしてどれだけ性能が向上するでしょうか。 以下に結果を示します。
exec time: 458917(us)
459ミリ秒とLinux版に対して20%ほど余計に時間がかかっています。
……忘れていました。 OSが無いということは、ただ開発が不便なだけではないのでした。起動直後のCPUは、ハードウェア浮動小数点演算器(VFP)やキャッシュなど、様々な機能がOFFになっています。 そのため起動時にはこれらの機能を適切に設定することで、ハードウェアの性能を存分に発揮できる状態にしてあげなければいけません。 それを行うコードもOSのカーネルに組み込まれています。
私は今回、VFPの設定は行いましたが、キャッシュの設定を行っていませんでした。そのためどうやら、キャッシュメモリの設定が行われているLinuxの方は、命令かデータがキャッシュに残っており、その差が実行時間の差に現れたのだと考えられます。
リベンジ——VFPを効率的に用いる最適化
このままでは悔しいので、BareMetal版コードの方をいじって高速化してみます。
Raspberry PiのCPUにはVFP(v2)というハードウェア浮動小数点演算器がついており、 これを使うと浮動小数点演算を高速に処理できます。早速やってみましょう。
通常、ARMのCPUで計算を行うには、CPUの持つ汎用レジスタ(r0,r1,...,r12)を用います。 しかし、VFPはCPUとは独立した装置なので、VFPの計算はVFPが持つレジスタ間のみで行われます。 そのため計算を行うには、値をメモリからVFPのレジスタにコピーし、結果をメモリにストアする作業が行われます。
一般的に、メモリのロード・ストアや、異なる装置間の値交換は、 レジスタのみを用いた演算に比べ低速です。 しかし、この遅い処理を一度にまとめて行うと、パイプラインが効いて速く処理できる場合があります。 この恩恵を最大限に受けられるようにしましょう。
ループのアンローリング
Raspberry PiのVFPは16本の64bitレジスタ(d0~d15)を持っているので、 最大16個の値を一度にまとめて処理して効率化できます。 これがどこに適応できるかというと、LU分解の行列Lを処理した以下の部分と、
// 行列Lの処理
double div_tmp = 1.0 / A[k][k];
/////////////////////////////////
////// 適応できる場所ここから //////
/////////////////////////////////
for (i=k+1; i<n; i++) {
// iで回す行方向ループ
// l_ik = a_ik / a_kk
A[i][k] = A[i][k] * div_tmp;
}
/////////////////////////////////
////// 適応できる場所ここまで //////
/////////////////////////////////
並列化の時にも触った、行列Uを処理する以下の部分です。
// 行列Uの処理
for (j=k+1; j<n; j++) {
// jで回す行方向のループ
// Tips: ここで値を変数に入れたほうが
// ループ内で参照するよりメモリアクセス回数が減ってお得
double a_jk = A[j][k];
/////////////////////////////////
////// 適応できる場所ここから //////
/////////////////////////////////
for (i=k+1; i<n; i++) {
// iで回す列方向のループ
A[j][i] = A[j][i] - A[k][i] * a_jk;
}
/////////////////////////////////
////// 適応できる場所ここまで //////
/////////////////////////////////
}
ここを一度にまとめて行うよう、次のように書き換えます。
/ 行列Lの処理
double div_tmp = 1.0 / A[k][k];
for (i=k+1; i<n-12; i+=12) {
// iで回す行方向ループ
double d4,d5,d6,d7,d8,d9,d10,d11,d12,d13,d14,d15;
// l_ik = a_ik / a_kk
d4 = A[i][k];
d5 = A[i+1][k];
d6 = A[i+2][k];
d7 = A[i+3][k];
d8 = A[i+4][k];
d9 = A[i+5][k];
d10 = A[i+6][k];
d11 = A[i+7][k];
d12 = A[i+8][k];
d13 = A[i+9][k];
d14 = A[i+10][k];
d15 = A[i+11][k];
d4 *= div_tmp;
d5 *= div_tmp;
d6 *= div_tmp;
d7 *= div_tmp;
d8 *= div_tmp;
d9 *= div_tmp;
d10 *= div_tmp;
d11 *= div_tmp;
d12 *= div_tmp;
d13 *= div_tmp;
d14 *= div_tmp;
d15 *= div_tmp;
A[i][k] = d4;
A[i+1][k] = d5;
A[i+2][k] = d6;
A[i+3][k] = d7;
A[i+4][k] = d8;
A[i+5][k] = d9;
A[i+6][k] = d10;
A[i+7][k] = d11;
A[i+8][k] = d12;
A[i+9][k] = d13;
A[i+10][k] = d14;
A[i+11][k] = d15;
}
for(;i<n;i++){
A[i][k] = A[i][k] * div_tmp;
}
// 行列Uの処理
for (j=k+1; j<n; j++) {
// jで回す行方向のループ
// Tips: ここで値を変数に入れたほうが
// ループ内で参照するよりメモリアクセス回数が減ってお得
double a_jk = A[j][k];
for (i=k+1; i<n-6; i+=6) {
// iで回す列方向ループ
double d4,d5,d6,d7,d8,d9;
// l_ik = a_ik / a_kk
d4 = A[k][i+0];
d5 = A[k][i+1];
d6 = A[k][i+2];
d7 = A[k][i+3];
d8 = A[k][i+4];
d9 = A[k][i+5];
d4 *= a_jk;
d5 *= a_jk;
d6 *= a_jk;
d7 *= a_jk;
d8 *= a_jk;
d9 *= a_jk;
A[j][i+0] -= d4;
A[j][i+1] -= d5;
A[j][i+2] -= d6;
A[j][i+3] -= d7;
A[j][i+4] -= d8;
A[j][i+5] -= d9;
}
for(;i<n;i++){
A[j][i] = A[j][i] - A[k][i] * a_jk;
}
}
このようにループを展開して高速化を行う手法を、ループのアンローリングといいます。
行列Lで行っていた計算は、
A[i][k] = A[i][k] * div_tmp;
このようなdiv_tmpと行列Aの要素1つの単純な掛け算なので、使用するVFPのレジスタ16以下に収まるよう、12回分(1+12 < 16)を一度に行うよう展開しています。 行列Uの計算と更新は、
A[j][i] = A[j][i] - A[k][i] * a_jk;
このようにa_jkと行列Aの要素を掛けた後、行列Aの別の要素へ引き算を行っています。 これはa_jkに1つ、行列Aの要素に2つレジスタを使うので、6回分(1+2*6 < 16)を一気に行うよう展開しています。
ループのアンローリング効果の確認
ループのアンローリングによる効果は、逆アセンブル結果を見れば明らかです。 以下にアンローリング後のコードを示すので、ダウンロードしてmakeを行ってください。
逆アセンブル結果は rpi-micon.disas に出力されます。このファイルを、アンローリング前と後で見比べてみてみます。
行列Lを処理していた部分の、アンローリング前のコードを示します。
809c: ed937b00 vldr d7, [r3] 80a0: ee277b06 vmul.f64 d7, d7, d6 80a4: ed837b00 vstr d7, [r3] 80a8: e2833c06 add r3, r3, #1536 ; 0x600 80ac: e15c0003 cmp ip, r3 80b0: 1afffff9 bne 809c <myLUsolver+0x34>
このコードはループを使って処理しているので、1変数ずつvldrでロード、vmul.f64で乗算、vstrでストアを繰り返しています。 しかしアンローリングを行うと、次のようにロードとストアが一列に並ぶコードになります。
8124: ed92ab00 vldr d10, [r2] 8128: ed919b00 vldr d9, [r1] 812c: ed9b8b00 vldr d8, [fp] 8130: ed9a0b00 vldr d0, [sl] 8134: ed991b00 vldr d1, [r9] 8138: ed982b00 vldr d2, [r8] 813c: ed953b00 vldr d3, [r5] 8140: ed944b00 vldr d4, [r4] 8144: ed9c5b00 vldr d5, [ip] 8148: ed93bb00 vldr d11, [r3] 814c: ed97cb00 vldr d12, [r7] 8150: ed906b00 vldr d6, [r0] 8154: ee2aab07 vmul.f64 d10, d10, d7 8158: ee299b07 vmul.f64 d9, d9, d7 815c: ee288b07 vmul.f64 d8, d8, d7 8160: ee200b07 vmul.f64 d0, d0, d7 8164: ee211b07 vmul.f64 d1, d1, d7 8168: ee222b07 vmul.f64 d2, d2, d7 816c: ee233b07 vmul.f64 d3, d3, d7 8170: ee244b07 vmul.f64 d4, d4, d7 8174: ee255b07 vmul.f64 d5, d5, d7 8178: ee2bbb07 vmul.f64 d11, d11, d7 817c: ee2ccb07 vmul.f64 d12, d12, d7 8180: ee266b07 vmul.f64 d6, d6, d7 8184: e59d3000 ldr r3, [sp] 8188: e283300c add r3, r3, #12 818c: e58d3000 str r3, [sp] 8190: e35300b3 cmp r3, #179 ; 0xb3 8194: e59d3008 ldr r3, [sp, #8] 8198: ed82ab00 vstr d10, [r2] 819c: ed819b00 vstr d9, [r1] 81a0: ed8b8b00 vstr d8, [fp] 81a4: ed8a0b00 vstr d0, [sl] 81a8: ed891b00 vstr d1, [r9] 81ac: ed882b00 vstr d2, [r8] 81b0: ed853b00 vstr d3, [r5] 81b4: ed844b00 vstr d4, [r4] 81b8: ed8c5b00 vstr d5, [ip] 81bc: ed83bb00 vstr d11, [r3] 81c0: e2833b12 add r3, r3, #18432 ; 0x4800 81c4: ed87cb00 vstr d12, [r7] 81c8: e2822b12 add r2, r2, #18432 ; 0x4800 81cc: ed806b00 vstr d6, [r0] 81d0: e2811b12 add r1, r1, #18432 ; 0x4800 81d4: e28bbb12 add fp, fp, #18432 ; 0x4800 81d8: e28aab12 add sl, sl, #18432 ; 0x4800 81dc: e2899b12 add r9, r9, #18432 ; 0x4800 81e0: e2888b12 add r8, r8, #18432 ; 0x4800 81e4: e2855b12 add r5, r5, #18432 ; 0x4800 81e8: e2844b12 add r4, r4, #18432 ; 0x4800 81ec: e28ccb12 add ip, ip, #18432 ; 0x4800 81f0: e58d3008 str r3, [sp, #8] 81f4: e2877b12 add r7, r7, #18432 ; 0x4800 81f8: e2800b12 add r0, r0, #18432 ; 0x4800 81fc: daffffc8 ble 8124 <myLUsolver+0xbc>
美しいですね。
連続してロードストアや演算を行っているので、パイプラインが効きやすいコードになっているはずです。
最適化結果の確認
ではこのプログラムを実行して、どれだけ最適化できたか確認してみましょう。 以下に結果を示します。
exec time: 417205(us)
アンローリングすると、その分コードサイズは増えてしまいますが、 命令の実効効率が良くなります。 その証拠に、アンローリング後のプログラムの実行時間は約40msも短くなりました。
しかし、Linux上で動かした結果には後一歩及びませんでした。リベンジ失敗です。
BareMetal版が勝つためには……
BareMetal版がLinuxで動かした結果に勝つためには、 すくなくともLinuxで行っているハードウェアの設定を、BareMetalでも行う必要があるでしょう。 しかし、その設定を行うため、CPUの資料やコードを読むコストを考えると、BareMetalでやるより、Linuxカーネルの設定を修正したほうが速いでしょう。
BareMetal版が優っている点としては、電源投入後すぐに実行され、結果が出ることでしょうか。 なので、電源投入から解が出るまでの時間で競えば、BareMetal版の勝利です。
今回のまとめ
・並列プログラミングの勉強には連立一次方程式ソルバがおすすめ
・並列化しても高速にならないどころか、逆に遅くなることもある
・OSの資源は偉大
・ループのアンローリングを適切に行うと、処理を高速化できる
次回は通信コストを削減して、再度、並列処理に挑戦する予定です
著者プロフィール
西永俊文 1992年生まれの情報系大学生。一人前のエンジニアを目指して日々勉強中。PDA全盛期の影響から、組み込み機器が好き。今欲しい物は、現代の技術で作られた物理キーボード付きで4インチ以下の小さなスマートフォン。著書に『BareMetalで遊ぶ Raspberry Pi』がある。
〈四コママンガ:囚〉

連載目次
2014-12-01 RaspberryPiクラスタ製作記 第0回「スパコンって本当にスゴイの?」
2014-12-01 PHASE/0のインストール方法
2014-12-16 RaspberryPiクラスタ製作記 第1回「スパコンを作ろう」
2014-12-16 Raspberry Piの初期設定
2014-12-29 RaspberryPiクラスタ製作記 第2回「スパコンで遊ぼう」
2014-12-29 HPLのインストール方法
2015-02-11 RaspberryPiクラスタ製作記 第3回「並列プログラミング」
2015-02-11 MPIを用いた並列プログラミングの概要
2015-02-11 LU分解アルゴリズムのおさらい
2015-03-01 RaspberryPiクラスタ製作記 第4回「BareMetal並列計算」